(Lady) GAGAN: Geometry-Aware Generative Adversarial Networks

Abstract

Deep generative models learned through adversarial training have become increasingly popular for their ability to generate naturalistic image textures. However, aside from their texture, the visual appearance of objects is significantly influenced by their shape geometry; information which is not taken into account by existing generative models. This paper introduces the Geometry-Aware Generative Adversarial Networks (GAGAN) for incorporating geometric information into the image generation process. Specifically, in GAGAN the generator samples latent variables from the probability space of a statistical shape model. By mapping the output of the generator to a canonical coordinate frame through a differentiable geometric transformation, we enforce the geometry of the objects and add an implicit connection from the prior to the generated object. Experimental results on face generation indicate that the GAGAN can generate realistic images of faces with arbitrary facial attributes such as facial expression, pose, and morphology, that are of better quality than current GAN-based methods. Our method can be used to augment any existing GAN architecture and improve the quality of the images generated. [PDF] [ArXiv]

BibTex:

@inproceedings{kossaifi2018gagan,
    author = {J. Kossaifi and L. Tran and Y. Panagakis and M. Pantic},
    booktitle = {IEEE Conference on Computer Vision and Pattern Recognition (CVPR)},
    title = {GAGAN: Geometry-Aware Generative Adversarial Networks},
    year = {2018},
}

Show me your Poker face

By changing the shape parameters a face following that shape is generated (1). Notice how Alejandro (row 1) starts smiling when we vary the corresponding shape parameter. More complex movements can be obtained by varying more than one shape parameter, as observed with Donatella, last row.

Conversely, by leaving it fixed and changing only the non-geometrical prior, GAGAN can generate various appearances while keeping a straight (fixed, really) face (2).

Varying only the shape parameters

Varying only the non-geometric parameters

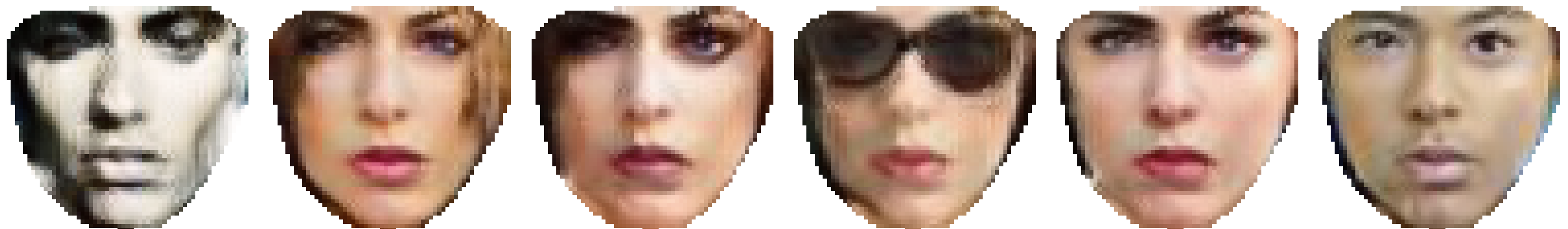
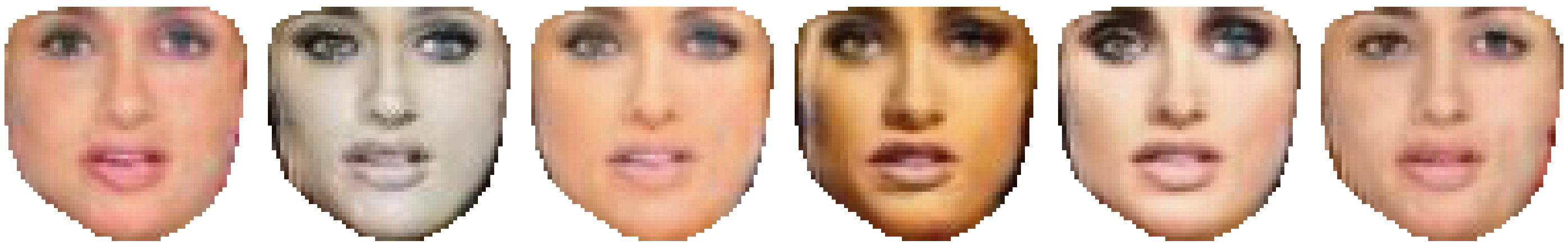
Bore me with the details

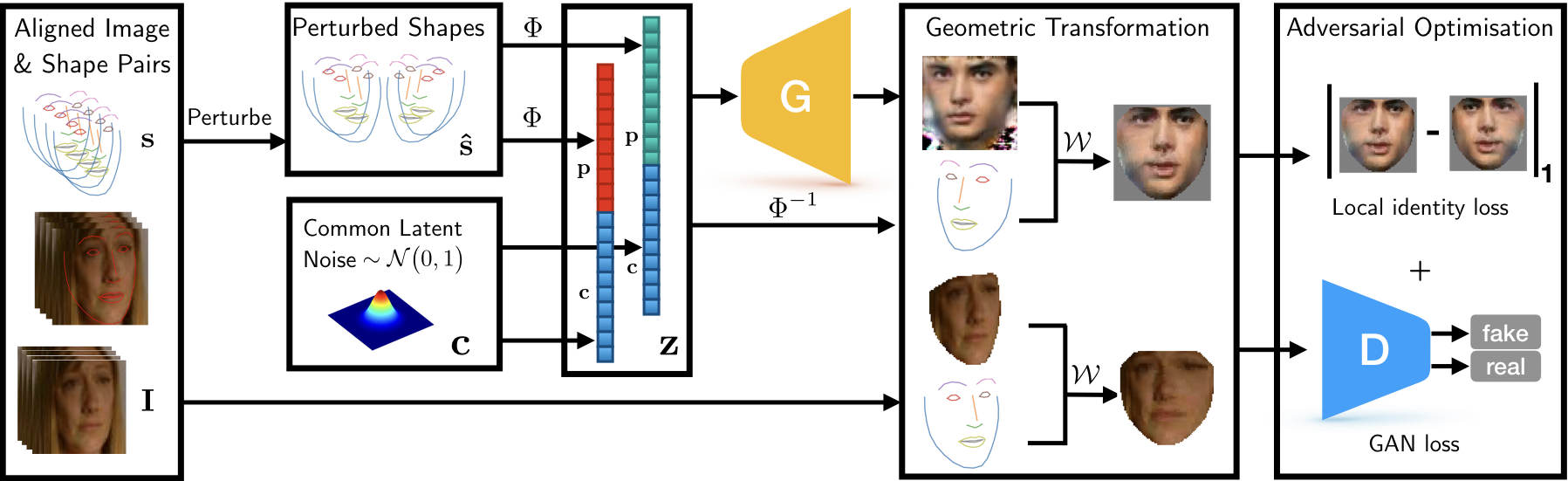
1. For each training image \(\mathbf{i}\), we leverage the corresponding shape \(\mathbf{s}\). using the geometry of the object, as learned in the statistical shape model, perturbations \(\mathbf{\hat{s}}_1, \cdots, \mathbf{\hat{s}}_n\) of that shape are created.
2. these perturbed shapes are projected onto a normally distributed latent subspace using the normalised statistical shape model. that projection \(\phi\left(\mathbf{s}\right)\) is concatenated with a latent component \(\mathbf{c}\), shared by all perturbed versions of a same shape.
3. the resulting vectors \(\mathbf{\hat z}_1, \cdots, \mathbf{\hat z}_n\) are used as inputs to the generator which generate fake images \(\mathbf{\hat i}_1, \cdots, \mathbf{\hat i}_n\). the geometry imposed by the shape prior is enforced by a geometric transformation \(\mathcal{w}\) (in this paper, a piecewise affine warping) that, given a shape \(\mathbf{\hat s}_k\), maps the corresponding image \(\mathbf{\hat i}_k\) onto the canonical shape. these images, thus normalised according to the shape prior, are classified by the discriminator as fake or real. the final loss is the sum of the GAN loss and an \(\ell_1\) loss enforcing that images generated by perturbations of the same shape be visually similar in the canonical coordinate frame.

The shape model

The shape model is an efficient way to model the structure of the face. I used it a lot in my work on Active Appearance Models (AAMs), for landmarks localisation. The general idea is to represent the shape of a face as a linear model, by applying PCA to a set of aligned facial shapes.

The components of the model can be interpreted as modeling pose (components 1 and 2), smile/expression (component 3), etc.

Enforcing the geometry: piecewise affine warping

Also known as motion model in the AAM literature, the piecewise affine warping maps the pixels from any shape onto a canonical shape. The main advantage is that a set of object, for instance faces, in different poses and with different shape can be easily compared once mapped onto the canonical shape. This allows to also implicitely check whether the face is correctly aligned with the corresponding landmarks.

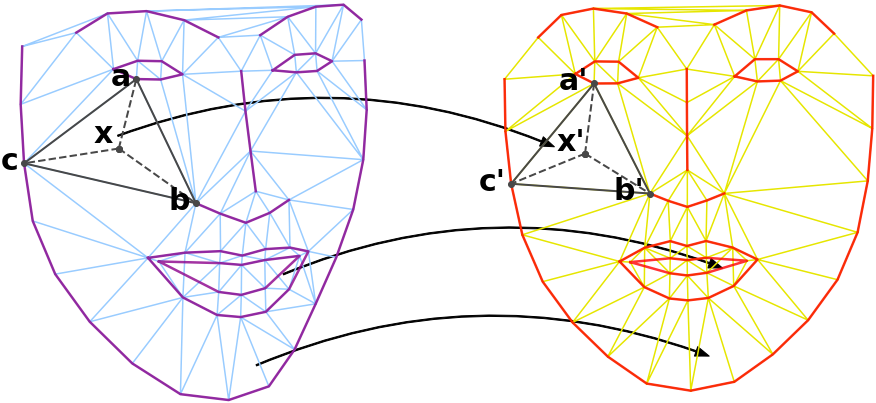
The piecewise affine warping works by first triangulating both shapes, typically as a Delaunay triangulation. The points inside each simplex of the source shape are then mapped to the corresponding triangle in the target shape, using its barycentric coordinates in terms of the vertices of that simplex, and the corresponding value is decided using the nearest neighbor or interpolation.